인접 리스트(Adjacency List), 인접 행렬(Adjacency Matrix)

인접 리스트(Adjacency List)란?

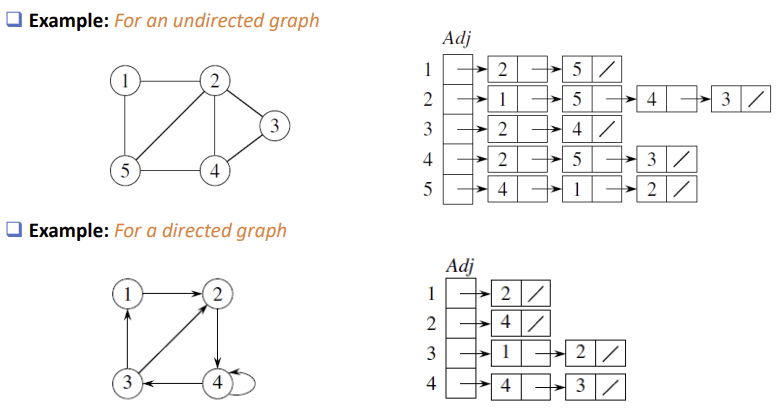
인접 리스트(Adjacency List)는 그래프를 표현하는 또 다른 방법으로, 각 정점에 인접한 정점들을 리스트로 저장하는 자료구조를 의미한다.

• 정점 번호나 이름을 key로, 인접 정점들의 리스트를 value으로 저장한다.
• 희소(sparse)한 그래프에서 공간 효율적이다.
• 정점의 인접 정점을 쉽게 찾을 수 있다.
• 특정 간선의 존재를 확인하는 데에는 시간이 오래 걸린다.

코드 예시

graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

인접 행렬(Adjacency Matrix)이란?

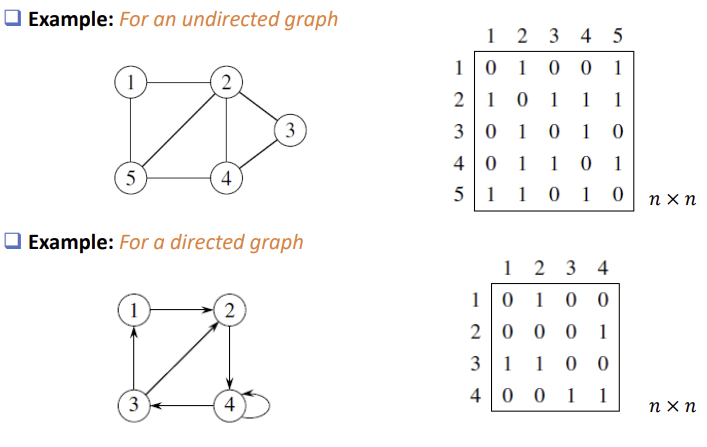
그래프에서 정점과 간선의 관계를 나타내는 bool 타입의 n x n 정사각형 행렬을 의미한다.

각 정점(vertex)는 0 또는 1이라는 값을 가지는데, 0은 두 정점 사이의 경로가 없음을 의미하고, 1은 두 정점 사이의 경로가 있음을 의미한다.

코드 예시

우선 2차원 배열을 생성합니다.

list comprehension 사용

row, cols = 5,5

matrix = [[0 for _ in range(cols)] for _ in range(rows)]
print(matrix,end="")

numpy 사용

import numpy as np

rows, cols = 5, 5
matrix = np.zeros((rows, cols), dtype=int)

matrix[0][1] = 1
matrix[0][4] = 1
matrix[1][0] = 1
matrix[1][2] = 1
matrix[1][3] = 1
matrix[1][4] = 1
matrix[2][1] = 1
matrix[2][3] = 1
matrix[3][1] = 1
matrix[3][2] = 1
matrix[3][4] = 1
matrix[4][0] = 1
matrix[4][1] = 1
matrix[4][3] = 1

print(matrix)

출력

[[0 1 0 0 1]
 [1 0 1 1 1]
 [0 1 0 1 0]
 [0 1 1 0 1]
 [1 1 0 1 0]]

예를 들어, 0번 노드에서 1번 노드로 가는 단방향 경로를 표현할 경우

matrix[0][1] = 1

0번 노드에서 1번 노드로 가는 양방향 경로를 표현할 경우

matrix[0][1] = 1
matrix[1][0] = 1

인접 리스트 vs 인접 행렬

특성	인접 리스트	인접 행렬
메모리 사용	O(V + E)	O(V^2)
간선 존재 확인	O(degree(v))	O(1)
모든 간선 확인	O(V + E)	O(V^2)
정점 추가	O(1)	O(V^2)
간선 추가	O(1)	O(1)
정점 삭제	O(V + E)	O(V^2)
간선 삭제	O(degree(v))	O(1)
공간 효율성	희소 그래프에 효율적	밀집 그래프에 효율적
구현 복잡도	상대적으로 복잡	간단
그래프 순회	O(V + E)	O(V^2)
가중치 표현	추가 정보 저장 필요	자연스럽게 표현 가능
적합한 상황	• 희소 그래프 • 정점/간선 추가가 빈번 • 전체 간선 탐색이 필요	• 밀집 그래프 • 간선 존재 확인이 빈번 • 정적인 그래프

선택 기준

1. 그래프가 희소하다면 인접 리스트가 유리하다.
2. 간선의 존재를 자주 확인해야 한다면, 인접 행렬이 유리하다.
3. 메모리가 제한적이라면 인접 리스트를 고려한다.
4. 정점과 간선의 추가/삭제가 빈번하다면 인접리스트가 유리하다.

보통은 인접 리스트를 많이 쓴다고 한다. 문제에서 sparse한 그래프가 많이 나오기 때문이다!