BFS(Breadth-First Search), DFS(Depth-First Search)

Breadth-First Search (BFS)란?

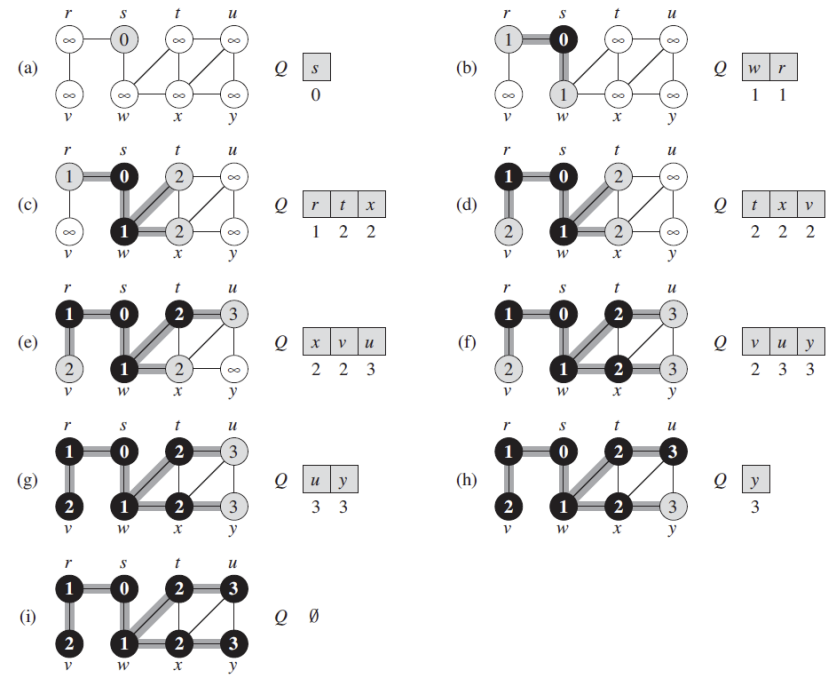
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어진 정점을 나중에 방문하는 탐색 방법이다.

동작 방식은 다음과 같다.

• 큐(Queue)를 사용해 구현한다.
• 시작 정점을 큐에 넣고 방문 표시를 한다.
• 큐에서 정점을 꺼내 그 정점과 인접한 모든 미방문 정점을 큐에 넣고 방문 표시를 한다.
• 큐가 빌 때까지 이 과정을 반복한다.

수도 코드 예시

특징

• 그림 처럼 같은 레벨의 노드들을 먼저 탐색한 후 다음 레벨로 넘어가는 특징을 가진다.
• 가중치가 없는 그래프에서 최단 경로를 찾을 수 있다.
• 모든 정점을 방문하는 완전 탐색의 특징을 가진다.

시간 복잡도

• 인접 리스트: O(V+E) (V는 정점의 수, E는 간선의 수)
• 인접 행렬: O(V^2)

사용 사례

• 최단 경로 문제
• 네트워크 분석
• 웹 크롤링
• 소셜 네트워크 관계 분석

장단점

• 장점: 최단 경로를 보장하고, 노드 간 최단 거리 탐색에 유용하다.
• 단점: 모든 노드를 저장하기 때문에, 메모리 사용량이 크다.

Depth-First Search (DFS)란?

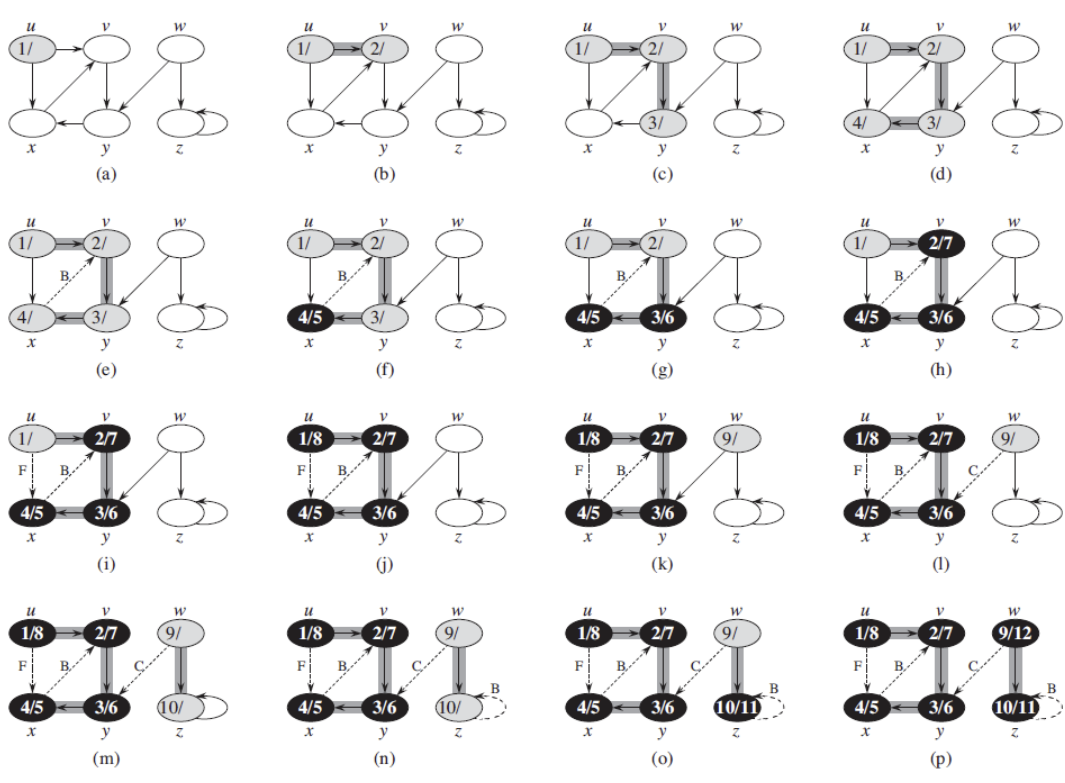
그래프의 한 정점에서 시작하여 가능한 한 깊이 들어가면서 탐색하는 방법이다.

동작 방식은 다음과 같다.

• 스택(Stack)이나 재귀(Recursion)를 사용해 구현한다.
• 시작 정점을 방문하고 표시한다.
• 현재 정점과 인접한 미방문 정점을 찾아 방문한다.
• 더 이상 방문한 정점이 없으면 이전 정점으로 돌아간다.

수도 코드 예시

특징

• 백트래킹: 더 이상 탐색할 곳이 없으면 이전 단계로 돌아간다.
• 메모리 효율성: BFS에 비해 적은 메모리를 사용한다.
• 경로 탐색: 모든 경로를 탐색하는 데 유용하다.

시간 복잡도

• 인접 리스트: O(V+E) (V: 정점 수, E: 간선 수)
• 인접 행렬: O(V^2)

사용 사례

• 미로 찾기
• 위상 정렬
• 연결 요소 찾기
• 사이클 탐지

장단점

• 장점: 구현이 간단하고 메모리 사용이 적다.
• 단점: 최단 경로를 보장하지 않고, 무한 루프에 빠질 수 있다.

DFS vs BFS

특성	DFS (깊이 우선 탐색)	BFS (너비 우선 탐색)
탐색 방식	한 경로를 끝까지 탐색	현재 정점과 가까운 정점부터 탐색
구현 방법	스택 또는 재귀 함수	큐
메모리 사용	일반적으로 적음	일반적으로 많음
최단 경로	보장하지 않음	가중치 없는 그래프에서 보장
완전 탐색	모든 경로 탐색에 유용	레벨 순서 탐색에 유용
무한 그래프	무한 루프 가능성	단계별 탐색 가능
적합한 문제	• 경로 존재 여부 • 사이클 탐지 • 위상 정렬 • 미로 찾기	• 최단 경로 문제 • 네트워크 유량 • 연결 요소 찾기 • 이진 트리 레벨 순회
시간 복잡도	O(V + E)	O(V + E)