[NLP] LLM의 양자화와 여러 방법론(QAT, AWQ)

Posted Sep 15, 2024

9 min read

개요

최근 LLM의 모델의 크기는 기하 급수적으로 증가하고 있습니다.

단순한 예로, GPT-3는 1750억개의 파라미터를 가지고 있으며 이는 엄청난 양의 저장 공간과 메모리를 필요로 합니다.

이처럼 큰 모델은 추론 시 많은 계산 리소스를 필요로 하며, 이는 높은 운영 비용과 긴 처리 시간으로 이어저 사용자의 만족도를 떨어트리는 결과로 나타납니다.

특히 최근에는 챗봇과 같이 실시간 응답이 필요한 애플리케이션과 엣지 디바이스에서의 AI 활용이 트랜드가 되면서 제한된 메모리 안에서 빠른 추론 속도를 가지고, 모델을 구동할 필요가 있었고, 이를 위한 LLM 양자화 기술의 중요성이 부각되었습니다.

양자화란?

그렇다면 양자화란 무엇인지 알아보도록 합시다.

양자화의 기본 원리는 연속적인 값을 이산적인 값으로 매핑하는 것입니다. LLM 컨텍스트에서 이는 주로 부동소수점 값을 정수값으로 변환하는 과정을 의미합니다.

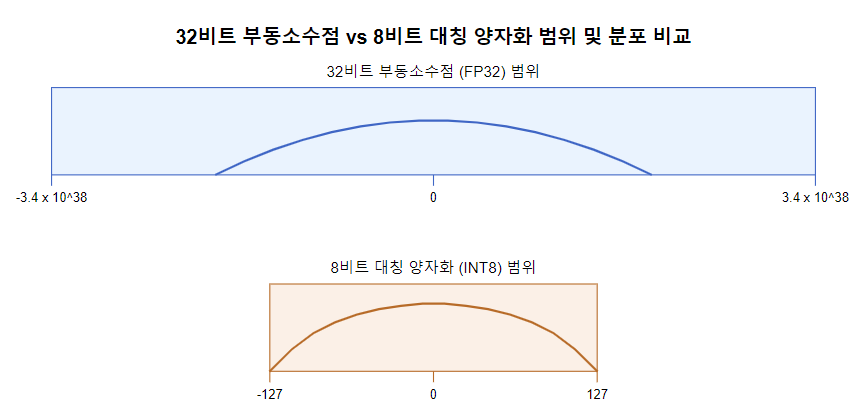
일반적인 LLM에서 가중치(weight)와 각 노드의 활성화(activation) 출력값은 32비트 부동소수점 형식으로 저장됩니다. 이 형식은 넓은 범위의 값을 높은 정밀도로 표현할 수 있지만, 많은 저장 공간과 계산 리소스를 필요로 합니다.

양자화 진행과정은 다음과 같습니다.

1. 각 층의 가중치와 출력 값의 최솟값, 최대값, 평균, 표준편차 등을 계산

전체 데이터셋이나 대표적인 샘플을 사용해 모델을 실행합니다. 각 층의 가중치와 활성화 값의 최소값, 최대값, 평균, 표준편차 등을 계산합니다.

2. 부동소수점 값을 정수로 변환할 때, 사용할 스케일 팩터를 결정

이 스케일은 양자화의 정밀도와 표현 가능한 범위에 직접적인 영향을 미치게 되는데, 작은 스케일의 더 정밀하지만 좁은 범위를 다루고, 큰 스케일은 더 넓은 범위를 다루지만 정밀도가 떨어집니다.

3. 결정된 스케일을 사용해 실제 부동소수점 값을 정수값으로 변환

클리핑을 통해 범위를 벗어나는 값들을 최대/최소 허용값으로 처리합니다. 0을 표현하는 제로 포인트 값을 별도로 정의해서, 비대칭 분포를 더 잘 표현할 수 있습니다.

결과

그림을 살펴보면, FP32 히스토그램은 대부분의 값이 0 주변에 집중되어 있지만, INT8 히스토그램은 이에비해 더 균일한 분포를 보여줍니다. 이는 양자화가 대부분의 중요한 값들을 보존하면서, 저장 공간과 효율성을 크게 향상시켰음을 보여줍니다.

예시 코드

  
import numpy as np

def symmetric_quantize_fp32_to_int8(fp32_matrix):
    # 최대 절대값 계산
    abs_max = np.max(np.abs(fp32_matrix))
    
    # 스케일 계산 (127을 사용하여 -127에서 +127 범위 사용)
    scale = abs_max / 127
    
    # 양자화 함수
    def quantize(x):
        return np.clip(np.round(x / scale), -127, 127).astype(np.int8)
    
    # 행렬 양자화
    quantized_matrix = quantize(fp32_matrix)
    
    # 역양자화 함수 (검증용)
    def dequantize(q):
        return q.astype(np.float32) * scale
    
    return quantized_matrix, scale, dequantize

출력 결과

원본 FP32 행렬:
[[-0.41406283 -0.01147755 -0.3392236  -0.6136786  -0.9619631 ]
 [ 0.34641847 -0.88415116 -0.9265099   0.01941179  0.3098219 ]
 [ 0.11344093 -0.49985033  0.27824652  0.8460101  -0.7981963 ]
 [ 0.67043334  0.64176756  0.29625052  0.511238    0.75581086]
 [ 0.9031928   0.17282692  0.9180173   0.4420913  -0.74508035]]

양자화된 INT8 행렬 (대칭적):
[[ -55   -2  -45  -81 -127]
 [  46 -117 -122    3   41]
 [  15  -66   37  112 -105]
 [  89   85   39   67  100]
 [ 119   23  121   58  -98]]

스케일: 0.0075745126232504845

역양자화된 행렬:
[[-0.4165982  -0.01514903 -0.34085307 -0.6135355  -0.9619631 ]
 [ 0.3484276  -0.88621795 -0.92409056  0.02272354  0.310555  ]
 [ 0.11361769 -0.49991783  0.28025696  0.8483454  -0.79532385]
 [ 0.67413163  0.6438336   0.29540598  0.50749236  0.75745124]
 [ 0.901367    0.1742138   0.916516    0.43932173 -0.74230224]]

평균 제곱 오차: 4.972453098162077e-06

출력 결과를 살펴보면, 원본 행렬의 ‘-0.41406283’ 값은 양자화와 역양자화를 거치며 ‘-0.4165982’라는 값으로 변하며 오차가 발생한다. 원본과 역양자화된 값의 평균 제곱 오차(MSE)를 계산하면 ‘4.972453098162077e-06’가 나오며 이는 매우 작은 오차로 정보가 잘 보존되었음을 나타낸다.

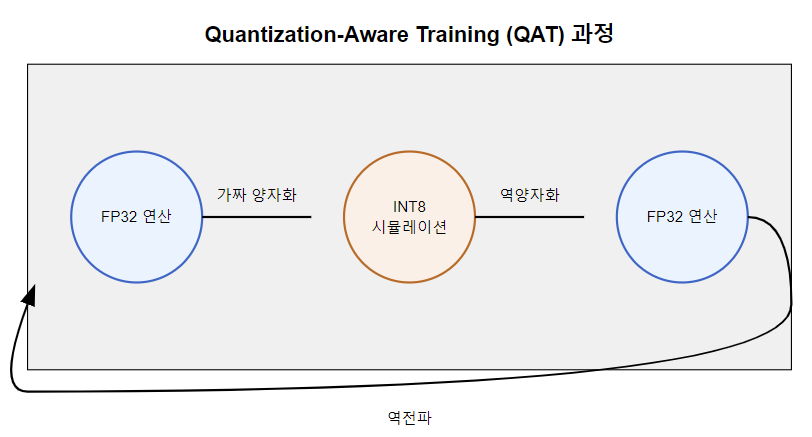
QAT(Quantization-Aware Training)

QAT는 훈련 중에 양자화의 효과를 시뮬레이션하고, 역전파 통해 양자화에 더 강건한 모델을 생성하는 방법입니다.

장점은 양자화로 인한 정확도 손실을 최소화한다는 점입니다. 또 양자화된 모델의 성능을 더 정확히 예측 가능합니다. 단점은 훈련 과정이 복잡하고 시간이 오래 걸린다는 점입니다.

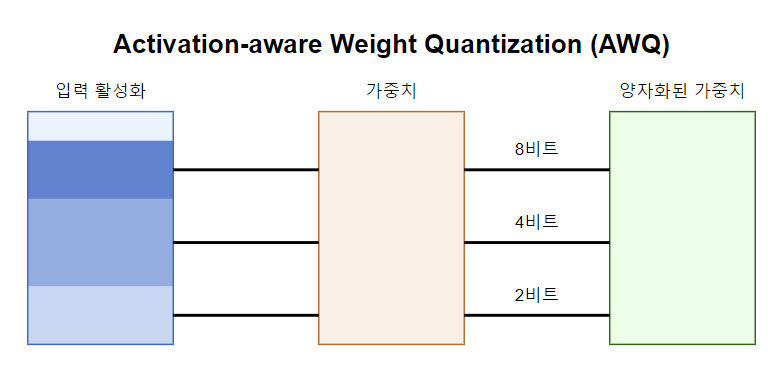
AWQ(Activation-aware Weight Quantization)

AWQ는 최근 제안된 효율적인 가중치 양자화 방법으로, 활성화(activation) 값의 특성을 고려해 가중치를 양자화 함으로써 성능 저하를 최소화 했습니다.

모델을 통해 샘플 데이터를 실행하여, 각 뉴련의 활성화 값을 수집합니다.
가중치를 여러 그룹(채널별 또는 행렬의 행별로)으로 나눕니다.
각 가중치 그룹의 중요도를 해당 그룹의 연결된 활성화의 중요도를 기반으로 계산합니다.
할당된 비트 수에 따라 각 가중치 그룹을 양자화합니다.

AWQ의 장점은 중요한 가중치에 더 많은 비트를 할당해 모델의 성능을 보존한다는 점입니다. 덜 중요한 가중치는 더 적은 비트로 표현해 전체 모델의 크기를 줄입니다. 또 각 레이어나 채널별로 다른 양자화 수준을 적용할 수 있다는 점도 장점입니다.

단점으로는 특수한 INT8/4 하드웨가 필요해 모든 환경에서의 배포는 제한됩니다.

study

This post is licensed under CC BY 4.0 by the author.